|
Long-Range Sound Propagation Group
Andrey K. Morozov, Timothy F. Duda, Ilya Udovydchenkov and John A. Colosi
|
|
|
Scientific Objective
Investigation of sound diffraction and scattering in long-range acoustic propagation with application to large scale ocean remote sensing and acoustic oceanography.
Concentration and Scattering of Sound in Long-Range Underwater Acoustic Channel
It is well known that sound concentrates at the depth of minimum sound velocity forming underwater channel. Concentration of acoustic energy along weakly divergent beams is another fundamental characteristic of long-range sound propagation. A geometrical acoustics interpretation of a weakly divergent beam is demonstrated in Fig. 1. Suppose that the source radiation width is confined by crossing trajectories of two acoustic rays shifted in the horizontal direction by a small distance roughly equal to the horizontal width of bundle; then the sound energy will spread in the narrow path bounded by those rays. A sound source with such directivity will form a narrow weakly divergent beam radiated at zero initial angle. The PE simulation of a 250Hz weakly divergent beam is shown in Fig. 2. The vertical dimension of the 2000m depth sound source aperture is roughly 150m. The sound from a source with the same aperture as Fig. 2 was numerically simulated in a homogeneous medium as shown in Fig. 3. A comparison between Figs. 2 and 3 shows that in a waveguide even a relatively small aperture sound source can concentrate energy in a very narrow beam. The rigorous normal mode analysis shows that the precise necessary condition of weakly divergent beams is the smooth extremum of ray cycle length dependence from emitted angle cosine. This condition is equivalent to the chaos degeneracy condition, known from ray chaos theory.
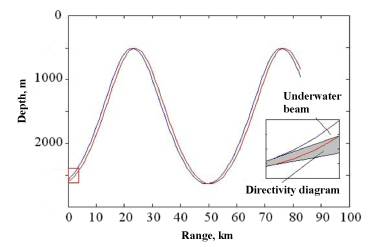
Fig. 1 Ray diagram of two paths displaced in range to demonstrate generation of a weakly divergent beam.
|
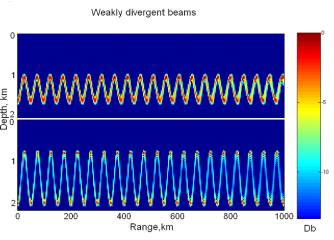
Fig. 2 Examples of parabolic equation calculations of two different weakly divergent acoustical beams (source was placed at depths of 1600m and 2000m). These simulations were carried out at 250Hz using the Munk canonical profile. Intensity is in dB referenced to the maximum intensity.
|
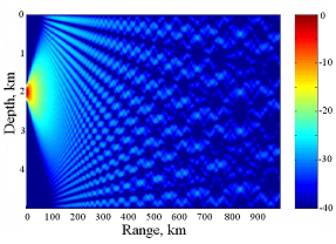
Fig. 3 Sound emitted by the same aperture as the 2000m source beam in Fig. 2 (lower), but here there is a constant background sound speed.
|
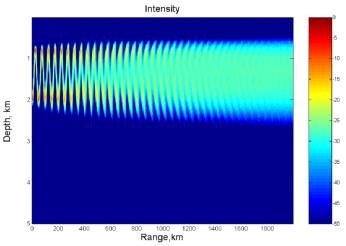
Fig. 4 Range evolution of mean intensity for the 250Hz beam with source depths of 2000m.
|
Acoustic energy in the ocean is significantly scattered by sound speed fluctuations induced by internal waves. Internal wave sound speed fluctuation is a Gaussian random process with the Garrett-Munk power spectrum. In the mixed layer near the ocean surface the sound scatters from fronts with a "spicy" structure. The subsurface fine structure with "spicy" (cold-fresh to hot-salty) fluctuation is more similar to a Poisson step-wise random process. The narrow beam is a useful tool for visual demonstration of wave scattering. Two different approaches are used for analysis of sound scattering in a random ocean: Monte-Carlo simulation and direct solving of differential equations for statistical moments in the Markov approach. The Monte-Carlo simulation is a very powerful method, which gives the correct answer for many complicated problems, but it is more expensive computationally. Directly solving differential equations for statistical moments is more computationally effective. The efficiency of that method for high frequencies is now under the investigation.
The Monte-Carlo simulation of narrow beam intensity spread is shown in Fig. 4. Monte Carlo stochastic simulation of acoustic scattering by internal waves allows analysis of the variability of a weakly divergent beam as a function of range and beam angle. A realistic Garrett-Munk internal wave model for the induced sound speed fluctuation was applied. The analysis shows that at the range near saturation the rate of physical entropy (a logarithmic measure of wave chaos complexity) for the complex envelope of the narrow beams decreases and converges to a small constant value which is approximately twice as large as the Kolmogorov-Sinai entropy or average Lyapunov exponent associated with the central ray of that beam. This rate is frequency independent and approximately equal to 0.04 bit/km. This correspondence suggests a full-wave manifestation of ray chaos, but only after saturation of the scintillation index has occurred. In spite of this correspondence, the simulated acoustical beams are not seen to expand exponentially (or explosively), but they expand diffusively.
Ray theory suggests that acoustic trajectories can be very sensitive to small perturbations of the initial conditions and media parameters (similar to light speckle sensitivity to a mirror rotations). For long distances this effect leads to growing acoustic field complexity and to chaos of rays trajectories. A methods based on perturbation of sound field propagation along non-disturbed ray trajectories are hardly can be proved for sound field simulation in a long-range propagation. Thats why parabolic equations and coupled-mode theory became the important instrumentation for study low-frequency sound field at a large range. A group of authors (Chernov, 1960; Tatarskii, 1971; Gorodetskaya, et. al., 1999) initially considered a stochastic equation in Markov approach for parabolic acoustic field approximation. Dozier and Tappert (1987) suggested statistical theory of sound propagation through a random internal wave field on a basis of normal mode decomposition and stochastic differential equations in a Markov approach. This approach was developed by Papanicolau and Kohler (1977, 1977). Note that coefficients of sound field mode decompositions in a random ocean are satisfying to a system of ordinary stochastic differential equations with random parameters. This form of stochastic equations was studied in an early works of Kubo (1962, 1963) and Van-Kampen (1974). The review on the subject can be found in books of Rytov et al. (1989), Ishumaru (1978).
Scattering of Sound in Shallow-Water Waveguides
The methodology described above has recently been applied to build a theory of mean sound levels in shallow water. In this situation, only a few modes propagate as low frequency, but the theory is similar. Theoretical expressions for cross-mode coherence versus range from a source and for mean sound intensity compare well with computational propagation simulation result, with results published in the Journal of the Acoustical Society of America.
Absorption of Sound in Seawater
Salty ocean water absorbs sound through “relaxation” chemical processes that are pressure dependent. In these processes, ions react as sound pressure waves pass (chemical reactions occur), reversing as the wave phase reverses. Important species are magnesium sulfate and borate. In these processes, volume changes associated with the reactions results in phase anomalies between water velocity oscillations and pressure oscillations (the water may be thought of as becoming compliant), resulting in acoustic energy loss. In the 1960’s through 1980’s considerable work was down to characterize the effects, with both at-sea experimentation and laboratory studies using various salty mixtures.
The borate ion based process is the dominant one for frequencies below a few kilohertz. It is also pH dependent, and therefore affords the opportunity to measure ocean acidity over long ranges via sound absorption measurements. To avoid misidentification of scattering-based sound losses and absorption, Jim and Worcester (1989) proposed a two-frequency method. We have recently updated analysis of this method to include recent advances in the knowledge internal-wave induced sound intensity fluctuations, which cause difficulty in measuring mean sound intensity, and thus also in measuring absorption and thus pH.
On another front, predictions of future increases of ocean acidity (reduction of pH) brought forth the hypothesis that the ocean would become noisier. We have studied this possibility using propagation modeling in hypothetical future ocean water conditions predicted with a climate model, Our results suggest that changes in ocean noise level would be slight, under the assumption that noise sources were to be unchanged (Udovydchenkov, Duda, Doney and Lima, 2010).
Pulse Broadening
In 2004 a study of pulse propagation in the 75-Hz frequency range over distance of 50 to 3200 km was made in the North Pacific Ocean. At this time, theories describing pulse broadening are being tested against the large and detailed data set. Results are to be submitted to a journal in 2011.
Scientific Instrumentation
Our instruments for an experimental research are deep-water, high-efficient sound sources and multi-element acoustic arrays. Further information, including experiments with long-range sound is available on the NPAL Web site: http://npal.ucsd.edu
|
Last updated: June 23, 2011
|





